Hi Juan,
Let me start by wishing you a Happy NewYear.
I’m thrilled to implement a fast simulation of the internal electric field of the device to improve its speed.A pn junction with a one-dimensional finite depletion region has a depletion width that can be directly solved by charge neutralization conditions without involving the diffusion equation.This suggests that there’s a way to directly solve the potential equation via similar charge neutralization conditions for 2D/3D devices.Based on this, in the present solution, is it the case that solving the diffusion equation is time consuming, and if so, is it possible to realize a fast simulation of the potential and electric field inside the device without solving the diffusion equation.
Kind regards
Hi @senzhao
Happy New Year! The normal simulation procedure is to do PotentialOnly solution, which is based on solving only for the electric field with the Poisson equation and assuming a flat fermi level. This is then used as the initial guess for the full drift diffusion equation solution. Would using this initial guess solution work for your purposes?
where
additionally the following is enforced at ohmic contacts:
I apologize for any sign mistakes in the above equations.
Hi Juan,
I am working with Sen about this problem. Our need is to simulate a pn-junction at high reversed bias voltage, not 0V (which corresponds to the condition of flat Fermi level). For the condition of 1D it is quite simple by estimating the width of depletion area, but we wonder is there a similar way to only calculate the potential for 2D or 3D devices, just like using sdevice in Sentaurus TCAD, but instead of Coupled(Poisson, Electrons, Holes) we want just execute Poisson.
To step further, we wonder if we could calculate the distribution of electrons and holes AFTER we have get the potential at high reversed-bias, to reduce running time.
Chenxi
Hi @Chenxi_Fu,
It is my intuition that doing a poisson only simulation with a high reverse bias should work, as long as you would not expect there to be any current, such as breakdown or avalanche conditions. The electron and hole distributions would then follow, as they come directly from the equations I mention above in a previous post.
The poisson-only is recommended in 1D, 2D, or 3D to reach an initial guess for drift diffusion simulation. For a case, like reverse bias and no current flow, I speculate that this solution may be sufficient for your needs.
How are you currently doing this in Sentaurus?
one thing that may or may not help with a voltage sweep is to disable the default log_damping in the example scripts.
https://forum.devsim.org/t/memory-leak-after-devsim-solve/348/2?u=juan
opts = get_equation_command(name="PotentialEquation", device=device, region=region)
opts['variable_update']="default"
equation(**opts)
Sorry for the late responce, Sen and I had some other works to do.
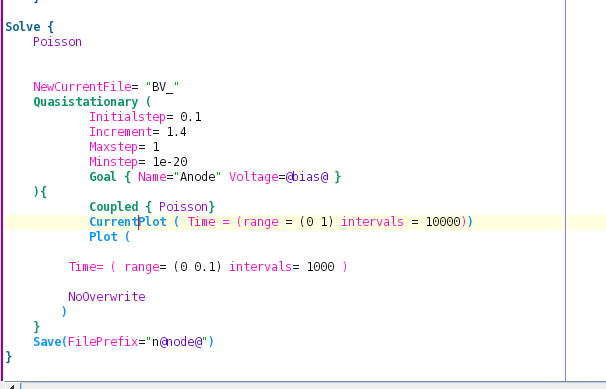
Here is an 1D simulation of a SiC LGAD (like a SiPM, but lower gain) device.
the Solve{} section:
Net doping of the device:
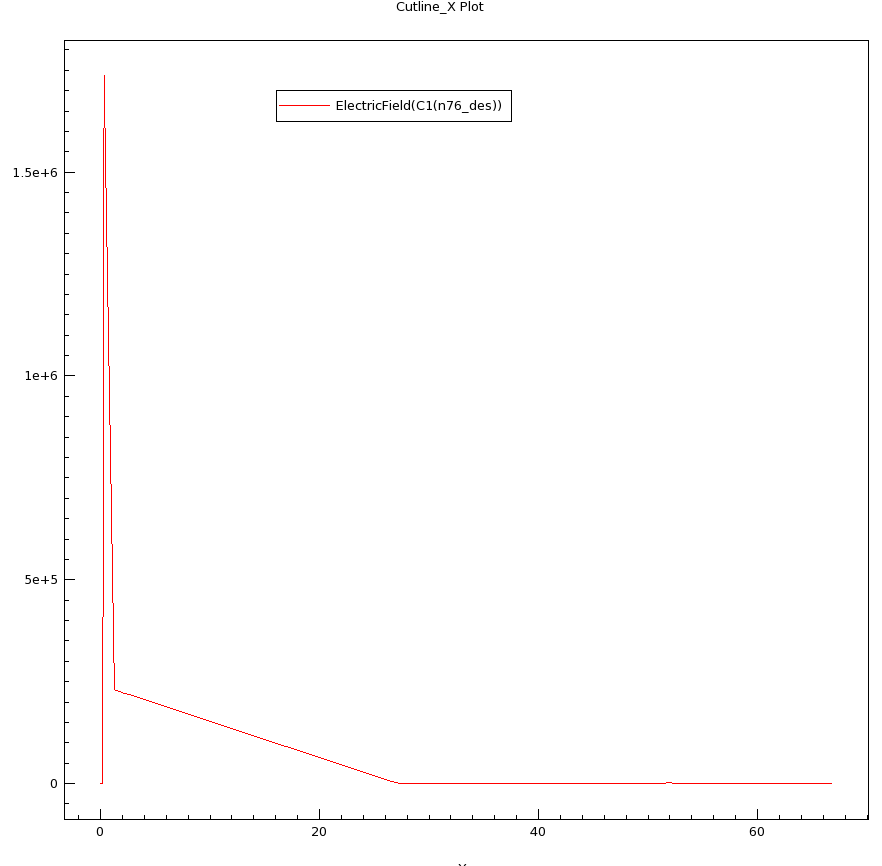
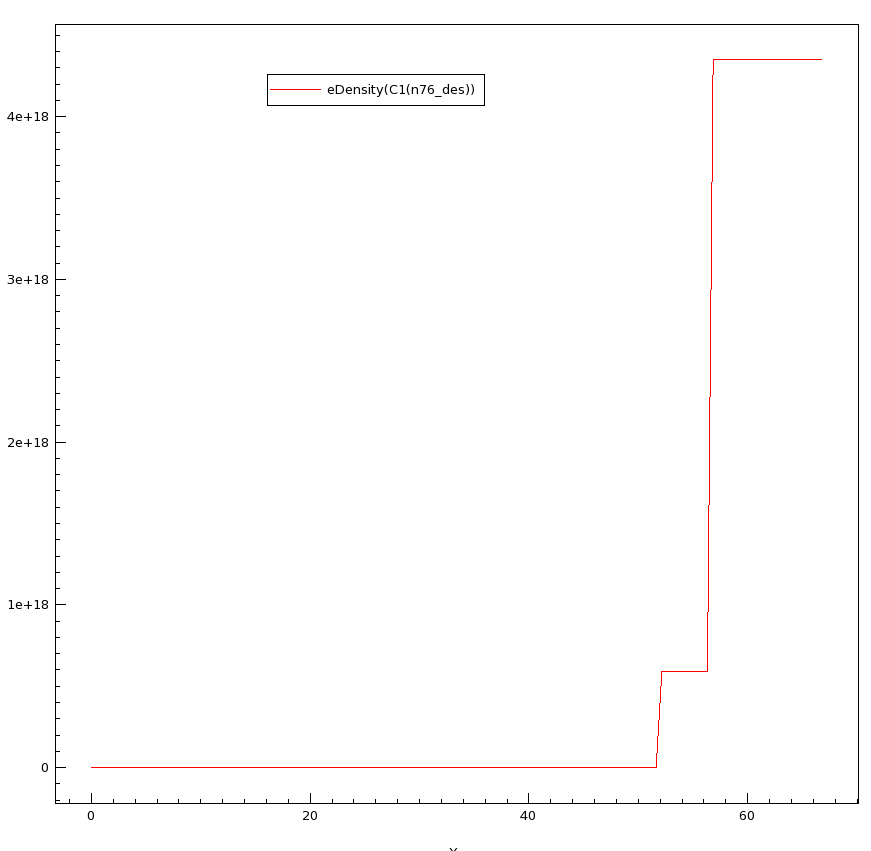
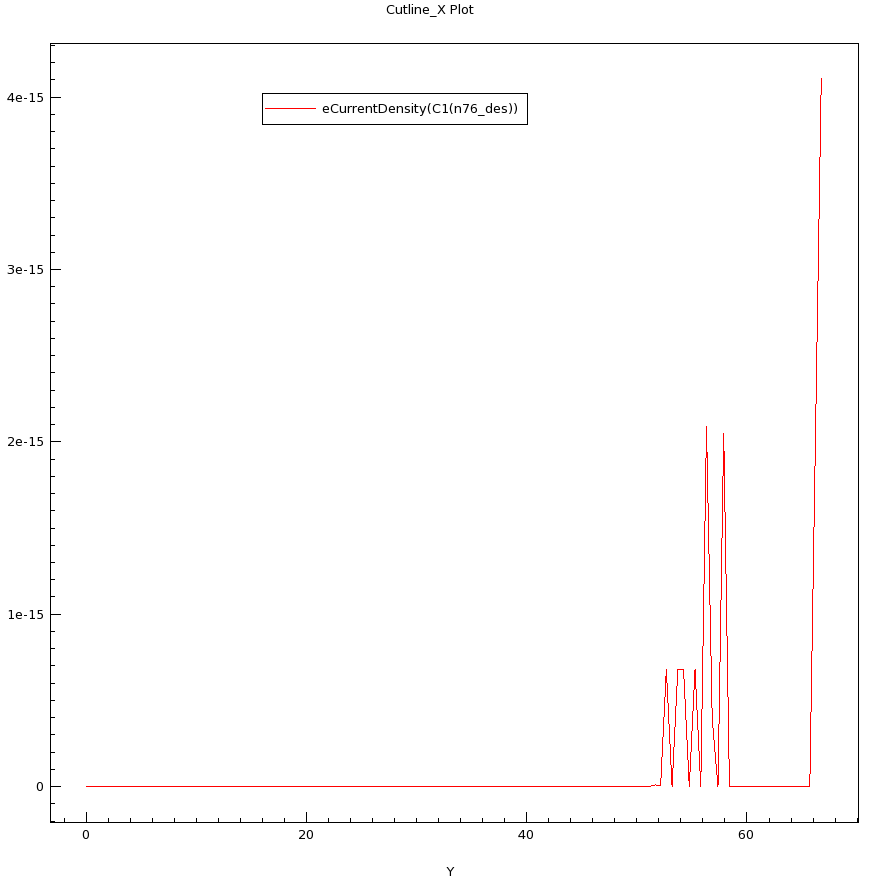
Results (the field, the electron density, and the deduced(?) electron current):
Hi @Chenxi_Fu
Thank you for sharing your results, which appear to come from Sentaurus. It is interesting that they are able to be able to calculate the current, which is essentially 0 throughout the device. The peaks in the current density plot are what appears to be a numerical artifacts, as a constant current throughout the device would be expected.
I assume something similar could be done in devsim by initializing the Electron and Hole densities from the poisson only solution, and calculating the current.