Hi Juan!
I want to use some realistic mobility model in the 2D MOS simulation. And I find that you have done already in your 3D MOS simulation. Actually, I am reading your code, but I want some suggestion that if you know how to apply the model in the 2D MOS simulation? Which part of original code in the 2D simulation should I replace and which part should I add? Sorry to bother you, I just want to do it quickly.
Please see this paper for a description of the model:
https://doi.org/10.36227/techrxiv.14129081.v3
The 3D simulation files are based on the ones used in the examples/mobility directory, During the review of the paper, I learned that it is much better to use the gradient in the quasi-fermi level for the velocity saturation. You can see this by comparing Figure 11 of the above paper with Figure 12 of this paper (Previous version):
https://doi.org/10.36227/techrxiv.14129081.v2
If you are not interested in the Lucent mobility model considering the transverse electric field, I would focus on modifying the velocity saturation for the quasi-fermi level gradient as the driving force. The code should be fairly easy to port over from the 3D mos repository and should work in both 2d and 3d.
It may also be possible to substitute your 2d device into the 3d mos directory and use the same physics files after doing the other alterations.
Hi Juan!
Thanks for your reply! I have read your paper and your 3D MOS code. And I have known how to use the Klaassen model and velocity model to improve the my simulation.
I still have a question. I found you use element model to describe and solve the electron and hole current in the 3D MOS. But the edge model is used in the examples/mobility directory. What’s the difference? what condition should I use them?
Part of the code in simple_dd:
def CreateElectronCurrent(device, region, mu_n):
'''
Electron current
'''
EnsureEdgeFromNodeModelExists(device, region, "Potential")
EnsureEdgeFromNodeModelExists(device, region, "Electrons")
EnsureEdgeFromNodeModelExists(device, region, "Holes")
# Make sure the bernoulli functions exist
if not InEdgeModelList(device, region, "Bern01"):
CreateBernoulli(device, region)
#### test for requisite models here
# Jn = "ElectronCharge*{0}*EdgeInverseLength*V_t*(Electrons@n1*Bern10 - Electrons@n0*Bern01)".format(mu_n)
Jn = "ElectronCharge*{0}*EdgeInverseLength*V_t*kahan3(Electrons@n1*Bern01, Electrons@n1*vdiff, -Electrons@n0*Bern01)".format(mu_n)
# Jn = "ElectronCharge*{0}*EdgeInverseLength*V_t*((Electrons@n1-Electrons@n0)*Bern01 + Electrons@n1*vdiff)".format(mu_n)
CreateEdgeModel(device, region, "ElectronCurrent", Jn)
for i in ("Electrons", "Potential", "Holes"):
CreateEdgeModelDerivatives(device, region, "ElectronCurrent", Jn, i)
part of the mos_physics:
def CreateElementElectronCurrent(device, region, name, mobility_model, electric_field):
Jn = "ElectronCharge*{mobility_model}*EdgeInverseLength*V_t*kahan3(Electrons@en1*Bern01, Electrons@en1*EdgeLength*{electric_field}/V_t, -Electrons@en0*Bern01)".format(mobility_model=mobility_model, electric_field=electric_field)
CreateElementModel(device, region, name, Jn)
for i in ("Electrons", "Holes", "Potential"):
CreateElementModelDerivative(device, region, name, Jn, i)
The expression for the electron current is the same, both for an element model and an edge model. However, the element allows the use of the transverse field based mobility, in addition to an edge model based or a parameter.
By using the:
devsim.element_from_edge_model
command, the direction of current flow across the element can be estimated from the edge current based on only a constant or doping based mobility. This can then be used to calculate the electric field normal to the current direction. This normal electric field can then go into the mobility for calculating the final current.
In the mobility examples, the dot product of the electric field with the current can be used in the velocity saturation current. However, in the paper review, a reviewer pointed out that this is a bad estimate, and it is better to use the gradient of the quasi Fermi level on the edge instead.
Looking at devsim_3dmos/ieee/sweeps.sh, which was used to generate the paper results, it appears that the best option to use is: “–hfs --model” to correspond to your use case.
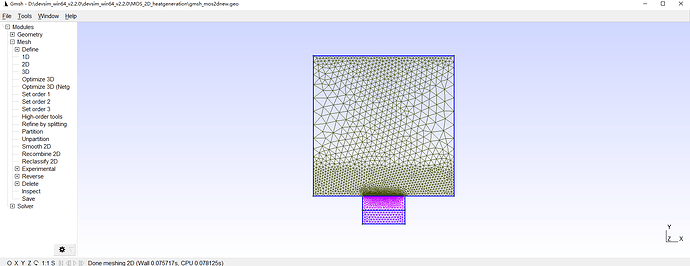
Thank you, Juan. For now, I don’t consider the surface mobility, so I still used the edge model to complete the simulation. And there is another question. I want to change the structure about the mos, like change the gate length. But after I change the gate length in .geo file and input it into gmesh, the output file .gmeh is very different from the original one.
The output file:
It seems some point information is lost. What should I do?
And after I change the structure, should I use the refinement in this link:
https://github.com/devsim/devsim_misc/tree/main/refinement
Hello @ghost
Please note that there are 3 files that can have the .msh extension.
- a devsim mesh file
- a gmsh version in the newest format
- a gmsh file in the gmsh 2 format
The last one should have this at the top of the file
$MeshFormat
2.2 0 8
$EndMeshFormat
and this can be created using this command line:
gmsh -2 -format 'msh2' myfile.geo -o myfile.msh
where you substitute the appropriate names for your .geo file and output .msh file respectively.
Please note that you also need to adjust the doping profile by adjusting similarly named parameters in the gmsh_mos2d_create to set the Donors and Acceptors
I suggest writing a tecplot format file and visualizing it to make sure that the doping profile makes sense.
write_devices(file='file.tec', format='tecplot')
The refinement scripts are useful to improve the quality of the simulation results. The ones in devsim_misc create a background mesh to improve the quality of the mesh by running it through gmsh multiple times. Please see the README.md file for info about the mos2d_refine.py mos2d_refine2.py script. It can be driven by the run.sh and run2.sh scripts.
Thank you, Juan!I will try it later.